The Trajectory Browser is intended to be a preliminary analysis tool for generating low-fidelity results. Mission designers would then be allowed to perform quick trade-off analysis to determine the viability of mission concepts.

Once the mission concept is nailed down, several tools are available to perform higher fidelity analysis. Some of them are listed below:

GMAT: Open source tool with a Graphic User Interface (GUI) and with documentation available. This tool can be customized through scripts made by the user and can perform detailed orbital and trajectory analysis.

AGI STK: Powerful software to compute detailed analysis related to orbital mechanics and also aircraft control. License required.

Orekit: Open source astrodynamics written in Java. They can be utilized to generate results for a wide variety of mission concepts.

The Trajectory Browser assumes impulsive maneuvers, which is the mathematical representation of an instantaneous change in the direction and magnitude of the spacecraft's velocity.

Low thrust maneuvers assume constant accelerations over large periods of time. These maneuvers are provided by, generally, electric propulsion systems with high specific impulses. At the moment, this option is not currently available.

The Trajectory Browser uses a Lambert solver to compute transfer orbits. This solver is a standard method in celestial mechanics to find Keplerian orbits that connect two position vectors with a given time of flight. This solution assumes that the only gravitational force applied to the problem is given by the Sun. For more accurate results, the gravity fields of the connected bodies plus other perturbations such as solar radiation pressure and third body gravity effects need to be taken into account.

All trajectories are pre-computed and stored in a database that contains all the solutions. In order to compute new trajectories to a non-existing object and/or if you wish to add a particular object that is not currently available, please contact us and we will have it included.

The database contains trajectories to more than 14,000 objects in the Solar System. In order to find solutions to them, you need to input the ID or the name in the 'Custom List' box.

The JPL Small-Body Search Engine generates data of objects in the Solar System based on the user input. This is useful to look for objects with particular characteristics. To find trajectories associated to them, you may use their official name or their 'SPK-ID' in the 'Custom List' box.

There is a limit of 100. For some particular queries, there are a large number of solutions. To avoid an overwhelmed page, the number of results are limited to a hundred. This does not mean that there are not more trajectories available. Therefore, it is necessary to tailor the search to find a particular trajectory.

All trajectories are computed under the assumption that injection occurs at a 200 km altitude Low Earth Orbit (LEO).

The DLA is computed by using the following equation, where epsilon is the angle that corresponds to the obliquity of the ecliptic and V is the velocity vector at injection.

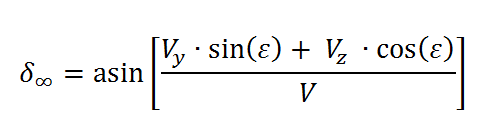
Figure I: Equation used to compute the Declination of the Launching Assymptote.

The altitude assumed for reentry is 200 km in an Earth-inertial frame.