| Overview | Limitations | Destination selection | Trajectory solver | References |
Trajectory Browser User Guide
Please refer to this section for a description of the main characteristics and limitations of this web application.
Overview
The Trajectory Browser is a search engine that allows a user to find impulsive trajectories to planetary bodies meeting specific constraints. The tool does not solve trajectories when queried, but instead pulls desired solutions from a pre-computed database of trajectories that is periodically maintained with some of the latest small-body discoveries. It is meant to be used as a first-cut survey to obtain preliminary accessibility results from a large population of planetary bodies. Results can then be used as initial guesses for trajectory design software yielding high-fidelity impulsive or low-thrust solutions.
It is important to note that there are several limitations to the trajectory solver due to various approximations and assumptions used to compute these trajectories, and therefore should not be used for any application other than a preliminary survey.
The Trajectory Browser currently holds trajectories for four classes of missions:
| Mission | Itinerary | |
|---|---|---|
| One-way | Flyby | Earth Departure → Destination Flyby |
| Rendezvous | Earth Departure → Destination Rendezvous | |
| Round-trip | Flyby | Earth Departure → Destination Flyby → Earth return |
| Rendezvous | Earth Departure → Destination Rendezvous → Destination Departure → Earth return | |
Limitations and approximations
Listed below is a summary of the Trajectory Browser's various limitations, approximations and sources of error:
Ephemeris uncertainty: A known small-body does not necessarily have a well-determined orbit. Orbit condition codes provide an indicator of how accurately a small-body's position can be predicted.
Ephemeris fidelity: For practical reasons, the highest-fidelity ephemerides that match observational data are not always used.
Trajectory configurations: The database holds solutions for direct transfers and simple gravity assists on outbound legs. More complex gravity assist maneuvers and other strategies may be used to find alternative trajectories not listed in the database.
Patched two-body approximation: A Lambert solver determines heliocentric transfer orbits without taking into account gravity due to planetary bodies, solar radiation pressure and other perturbations. ΔV and other velocities local to a planet are also evaluated with two-body dynamics, while small-bodies are assumed to have zero-mass.
Time space discretization: Launch and arrival dates for minimum-ΔV trajectory solutions can only be found to within a half time-step.
Global constraints: A user is limited to searching for a subset of trajectories computed using pre-determined constraints beyond the user's control.
Design trades: The database of trajectories is only set up to trade mission duration against total ΔV.
Destination selection
- Included bodies
The Trajectory Browser currently holds solutions for transfers from Earth to all planets and known Near-Earth Objects (routinely updated with latest discoveries). If there is a body or class of bodies not found on the Trajectory Browser but useful to your mission, please contact us with your suggestions.
- Query system
The number of displayed trajectories for a particular search is limited to a maximum of a hundred. Therefore, the users are required to tailor their searches to satisfy their needs. If ,for instance, a user wants to find trajectories to Venus and the entry settings are set in a way that the number of trajectories available exceeds the limit, only a hundred results would be displayed. The particular cases that are shown depends on the search. For example, a particular search may return trajectories sorted by time of flight from maximum to minimum. If the displayed trajectories reach the limit of a hundred, there may be solutions with shorter time of flights available. In this case, to find out, the search should be redefined to limit the duration to a certain maximum number that meets the user's mission requirements.
- Specifying a list of small-bodies
To search for trajectories from a specific subset of included bodies, check the 'Custom list' checkbox and enter a list of objects in the subsequent field of the Trajectory Browser search page. Objects may be entered by SPK-ID, asteroid number, name/designation, with one body per line as in Figure 1. For example, to search for trajectories to the asteroid Apophis, one may enter its SPK-ID '2099942', its asteroid number '99942' or simply its name 'Apophis'.
Figure 1: Three NEOs entered by SPK-ID, name and designationA custom list of small-bodies can be generated with the JPL Small-Body Search Engine. For example, one may use this tool to select all S-class NEOs by selecting the proper constraints and outputting SPK-IDs into a spreadsheet-usable CSV file. From the spreadsheet, simply copy the column of SPK-IDs to the Trajectory Browser's 'Destinations' field. Alternatively, include all Near-Earth Objects by checking the asteroid or comet boxes to include these objects, and optionally place additional constraints on absolute magnitude and orbit condition code.
- Absolute magnitude and approximate size
The absolute magnitude for objects listed in the Trajectory Browser is the H magnitude for asteroids and M2 nuclear magnitude for comets, when available. The listed size corresponds to the object's actual diameter if it is known, but since that is rarely the case for small-bodies, a range of diameters is given based on an assumed albedo of 0.05 to 0.25. Data for magnitudes and known diameters is obtained from the JPL Small-Body Database.
- Orbit condition code
The orbit condition code, also known as the U uncertainty parameter, is an integer between 0 and 9 indicating how well an object's orbit is known on a logarithmic scale, where 0 indicates a well-determined orbit.
Orbit condition codes are particularly important when computing spacecraft transfer trajectories several years or more after the latest observation, since the code indicates how the uncertainty of a small-body's position grows with time. Small-bodies with higher orbit condition codes imply inherently greater uncertainty in the existence and ΔV-values associated with trajectories to those bodies. Orbit condition codes can be reduced when more optical or radar observations become available.
Orbit
Condition CodeLongitude runoff
per decade0 < 1.0 arc seconds 1 < 4.4 arc seconds 2 < 19.6 arc seconds 3 < 1.4 arc minutes 4 < 6.4 arc minutes 5 < 28.2 arc minutes 6 < 2.1 degrees 7 < 9.2 degrees 8 < 40.7 degrees 9 > 40.7 degrees Table 2: Longitude uncertainty by orbit condition code. - Ephemerides
Ephemerides for small-bodies consist of state vectors sampled at one-year intervals from the JPL HORIZONS system. To compute position and velocity information at a given epoch, a weighted extrapolation of two-body propagation is used from the bounding state vectors.
The annual state elements provide sufficient ephemeris accuracy for most small-bodies in the context of a preliminary trajectory survey. However, this extrapolation suffers when a small-body makes a close planetary approach since a massive body will considerably perturb its orbit. Therefore, for a small number of near-Earth asteroids making close-approaches to the Earth or other massive bodies, a coarser sampling of state vectors is obtained around the close-approach event to provide improved accuracy for trajectories launching or returning near these close-approaches
Trajectory solver
- Lambert's problem [2]
- Trajectory survey [3]
- Itinerary
- Patched conic approximation [4]
- Launching segment
- Flyby segment
- Arriving segment
- Injection ΔV is directly related to C3 and represents the maneuver required for Earth-escape and insertion into a heliocentric orbit.
- Post-injection ΔV are all maneuvers required after injection such as flyby, rendezvous and departure ΔV's.
- Total ΔV is the sum of injection and post-injection ΔVs.
- Global trajectory constraints
- Saving user-specified constraints
- ΔV vs. Duration trade
- Detailed trajectory design
The transfer orbits stored in the Trajectory Browser are computed with a Lambert solver, an approximate but computationally-efficient method ideal for broad surveys of small-bodies. Lambert's problem for small-body heliocentric transfers can be stated as follows: given an Earth launch date and transfer duration to reach a small-body, determine the Keplerian transfer orbit connecting the two bodies.
The fundamental approximation made by Lambert's problem is that only the Sun's gravity is considered: the Earth and the small-body's gravitational influences are ignored as well as other large perturbing bodies such as Venus, Mars and Jupiter. A high-fidelity trajectory, beyond the scope of the Trajectory Browser, would also take into account third-body perturbations, solar radiation pressure, gravity losses during ΔV maneuvers and trajectory correction maneuvers (TCMs) due to imperfect state knowledge and modeling.
To determine which combinations of launch date and transit time yield low ΔV, the two-dimensional time space is first discretized into all combinations of (tlaunch, tarrival) pairs for a given time step. For every pair, Lambert's problem is then solved to compute a transfer trajectory launching from Earth and arriving at the small-body at the given dates. The changes in velocity (ΔV) required to leave Earth and arrive at the small-body can then be calculated.
If a (tlaunch, tarrival) couple requires a ΔV below a user-defined threshold, it is added to a list of acceptable trajectory solutions from Earth to that small-body. These solutions can be visualized on a plot of launch date vs. duration color-coded by ΔV, in what are colloquially known as 'porkchop plots' (Figure 2). The time step used for the discretization of the time domain is usually picked to be small enough to capture a trajectory sufficiently close to the local minimum of each porkchop given the Lambert solver's limitations. Further optimization of the local minimum is possible using various numerical techniques.
This process for finding low-ΔV opportunities from Earth to a given small-body is then repeated for all candidate bodies.
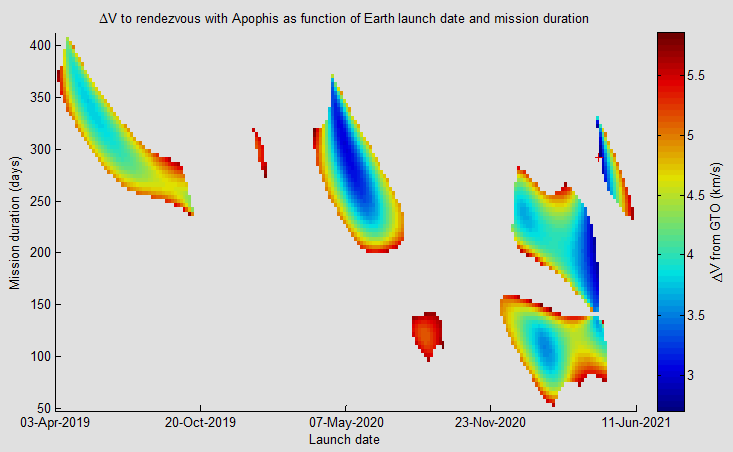
Figure 2: Example of a porkchop plot for rendezvous trajectories with 99942 Apophis.
The problem of computing round-trip trajectories is split in two: Earth→Small-Body and Small-Body→Earth trajectories are first evaluated separately. Each Earth→Small-Body trajectory is then iteratively matched to every Small-Body→Earth transfer and are combined to form a round-trip trajectory if they meet pre-defined constraints on the stay time at the small-body as well as total ΔV.
Flyby trajectories are similar to rendezvous trajectories without any requirement on the rendezvous ΔV. Computing trajectories for flyby return missions are more complex and require a three-dimensional time grid (tlaunch, tflyby, tarrival) with two Lambert transfers (Launch→Flyby and Flyby→Arrival).

Figure 3: Rendezvous trajectory with 99942 Apophis.
The Trajectory Browser lists the itinerary of each trajectory in the 'Route' column with the shorthand nomenclature in Table 3.
For example, the route 'EMA-AE' implies a round-trip mission to an asteroid with a Mars flyby on the outbound leg.
| Letter | Significance |
|---|---|
| A | Asteroid |
| C | Comet |
| E | Earth |
| M | Mars |
| V | Venus |
| - | stay |
The injection characteristic energy C3 is defined to be the square of the hyperbolic excess velocity V∞, which is the vector difference between Earth's velocity and the heliocentric orbit's velocity. Injection ΔV from a 200 km altitude Low Earth Orbit (LEO) is evaluated from the C3 using two-body dynamics.

Figure 4: Two-body Earth departure hyperbola.
The Declination of the Launching Asymptote (DLA) is obtained from the vector angle between V∞ and Earth's equatorial plane. The absolute value of the DLA is of significance to mission designers because it represents the minimum Earth orbit inclination required for injection, which can be limited by the launch site's geographic latitude.
The flyby ΔV for en-route gravity assists is calculated from the inbound and outbound V∞'s. For flybys of small-bodies on round-trip missions, the ΔV is evaluated from the vector difference of V∞'s. For planetary flybys, a two-body patched conic approximation is used to evaluate a ΔV impulse at periapsis and the required flyby altitude required to satisfy the inbound and outbound asymptotic boundary conditions, as sketched in Figure 5. A particular flyby scenario is rejected if the required periapsis is below the planet's atmosphere or surface. Note that no ΔV is required for events where the flyby is the last item on a mission's itinerary, as the spacecraft's trajectory is no longer relevant post-flyby.
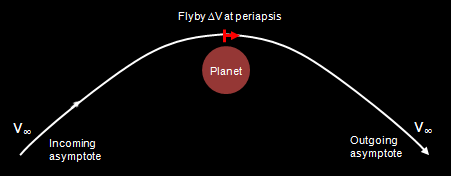
Figure 5: Two-body planetary flyby approximation.
The ΔV required for rendezvous with a small-body is calculated from the vector difference between the spacecraft and small-body's velocity vectors. This represents the maneuver required for the spacecraft to match the small-body's speed and direction.
Rendezvous ΔV for planetary bodies is the maneuver required a safe distance above the planet's atmosphere to reduce orbital velocity to escape (C3 = 0) assuming two-body dynamics. Depending on the nature of the mission, additional ΔV maneuvers not considered in the Trajectory Browser will be required to adjust the spacecraft's planetary orbit.
Earth reentry speed is obtained by two-body propagation from hyperbolic excess velocity to the reentry interface.
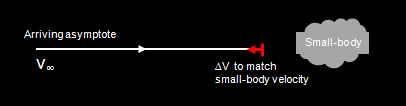
Figure 6: Arrival at a small-body assumed to have zero-mass.
A user performing a search in the Trajectory Browser is filtering through a database of trajectories with specific constraints on the destination, launch date, mission duration and ΔV. A user is however limited to searching a subset of pre-computed trajectories, since the trajectories entered into the database were themselves calculated with constraints in mind. This means that a user cannot set higher constraints than those used to generate the database. For example, if a mission's global constraint on post-injection ΔV is 5 km/s but the user specifies a maximum ΔV of 7 km/s, only trajectories with up to 5 km/s post-injection ΔV will be returned. Table 4 shows the global constraints for each mission class in the Trajectory Browser.
| Earth launch window | Jan-01-2010 to Jan-01-2040 |
|---|---|
| Maximum mission duration | 10 years for round-trip rendezvous 5 years for others |
| Minimum stay time at destination (round-trip rendezvous only) | 5-100 days depending on mission duration |
| Maximum total ΔV | 10 km/s for rendezvous 6 km/s for one-way flyby 7 km/s for round-trip flyby |
| Solver time-step | 5-16 days depending on mission duration |
To date, transfer segments that make up to two revolutions around the Sun have been implemented. Robotic rendezvous and sample-return missions include outbound transfers that flyby Venus, Earth or Mars. Earth flyby transfers (itineraries that begin with 'EE') use 2:1 resonance [5] with a small deep-space maneuver at aphelion included in the post-injection ΔV.
These constraints are meant to be high enough to cover realistic mission designs but not too high to maintain the trajectory database at a practical size. If you find one or more constraints to be limiting your mission design, you can voice your suggestion by contacting us.
For relatively short lists of user-entered destination candidates, the search results are returned in such a way that a user can bookmark the page, saving their specific constraints. For example, one may choose to bookmark the 180-day human rendezvous missions with specific ΔV constraints to regularly check for new candidates from recent NEO discoveries.
For most robotic missions, it is desirable to minimize the total mission ΔV to lower cost or maximize the science return, in which case the trajectory with the lowest ΔV is selected from each opportunity (or 'porkchop'). However for human spaceflight endeavors and some robotic missions, a mission designer will want to lower the mission duration at the cost of extra ΔV. To allow a user to trade total mission ΔV with duration, the locally optimal pareto frontier points of each 'porkchop' are stored in the Trajectory Browser database. A trajectory is deemed locally pareto-optimal if no other trajectory within a certain temporal radius has a lower ΔV and duration, as illustrated in Figure 7.
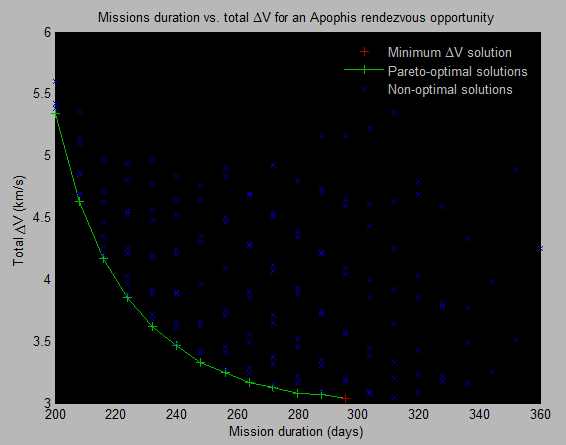
Figure 7: Apophis rendezvous porkchop replotted on a ΔV vs. duration graph,
showing the pareto-optimal solutions saved by the Trajectory Browser
To obtain the minimum ΔV trajectory of a given rendezvous opportunity, select the 'ΔV' minimizer in the Trajectory Browser options and relax the maximum duration constraint. To lower the duration at the cost of extra ΔV, simply reduce the duration requirement. Alternatively, one can choose to minimize the mission duration given a ΔV constraint. Figure 8 illustrates the difference between minimizing ΔV or mission duration along the pareto front.
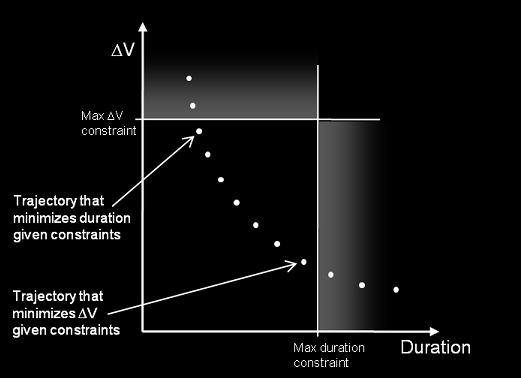
Figure 8: Pareto-optimal trajectories minimizing ΔV and mission duration given user-specified constraints.
To find the optimal trajectory across the desired launch date window, select the 'optima' option after selecting the parameter to minimize. For individual launch opportunities across a wide launch window, selecting the '1-yr local optima' option will return trajectories that are at most approximately one year apart. Selecting 'all trajectories' will return any trajectory in the database that satisfies the user's constraints.
It is important to understand the limitations of the Trajectory Browser with respect to design trades. While it is possible to crudely trade total ΔV with duration despite the limitation associated with discrete Lambert solver's time-steps, there are many more trades that are not available in the Trajectory Browser and are outside the scope of its use as a preliminary trajectory survey. For example, using numerical techniques one can trade C3 vs. post-injection ΔV vs. rendezvous stay time vs. DLA etc. A user cannot specify constraints on DLA or reentry speed since the trajectories in the database were selected only for a ΔV vs. mission duration trade, and will not give a fair representation of trajectories from other design trades.
The Trajectory Browser is meant to be a low-fidelity design tool for quickly scanning large populations of small-bodies. Once the desired opportunities are found, a mission designer may use the search results as initial guesses for impulsive or low-thrust high-fidelity trajectory design tools. NASA's In-Space Propulsion Technologies Program provides a listing of some trajectory optimization tools. General Mission Analysis Tool (GMAT) is space trajectory optimization and mission analysis system developed by NASA and private industry in the spirit of the NASA Vision.
References
Folkner, W., Williams, J., Boggs, D., The Planetary and Lunar Ephemeris DE 421, IPN Progress Report 42-178
Bate, R., Mueller, D., White, J., Fundamentals of Astrodynamics, Dover Publications, 1971, pp. 227-234
Foster, C., Daniels, M., Mission Opportunities for Human Exploration of Nearby Planetary Bodies, AIAA SPACE 2010, Anaheim, CA, AIAA 2010-8609
Bate, R., Mueller, D., White, J., Fundamentals of Astrodynamics, Dover Publications, 1971, pp. 357-381
Hollenbeck, G., New Flight Techniques for outer Planet Missions, AAS paper 75-087, 1975 AIAA/AAS Astrodynamics Specialist Conference

